We say that a frame "inherits" properties from its abstractions. This is implemented by having some function, e.g., get-attribute-value, that takes the name of some concept and some attribute, and returns the value for that attribute.

Single Inheritance

The algorithm for single inheritance, where every concept has at most one abstraction, is simple:

For example, consider the following hierarchy:

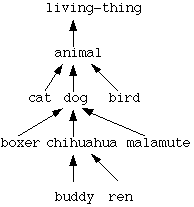
When asked for some attribute of buddy, the concepts would be searched in the order: buddy, chihuahua, dog, animal, living-thing.

Multiple Inheritance

Things get much more complicated as soon as we allow concepts to have more than one abstraction. Consider this hierarchy:

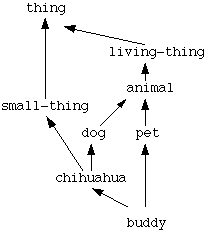
What's the right order now? In fact, there are many "right" orders.

The most important rule that the inheritance algorithm has to obey is that the most specific concept "wins." This means that

There is no a priori reason, however, to prefer inheriting from chihuahua before inheriting from pet. Though pet may seem more abstract in some sense than chihuahua, this is not captured in the relationships above. Syntactically, pet and chihuahua are immediate abstractions of buddy and that's all we know.

Side note: Rules for estimating the "abstractness" of a concept by the number of links from the root of the tree to the concept, only work if all parts of the tree are equally well developed. In fact, most abstraction hierarchies are quite unbalanced, with many layers of concepts in heavily used sections, and just a few concepts in others. Comparisons across sets of abstractions simply doesn't work in practice.

Using depth-first search

A depth-first traversal of the concepts above buddy would generate the following list:

buddy chihuahua small-thing thing dog animal living-thing thing pet animal living-thing thing

Problems with depth-first search

Using this list as an ordering for inheritance has several problems. First, some concepts, such as animal and thing, appear more than once. Second, some concepts appear before concepts that they are abstractions of. For example, thing appears before dog. That means that if we search the list from left to right for an attribute, we may find the value on thing, say, before we find the one we want on dog.

A multiple inheritance algorithm

Concepts appear more than once and out of order when we "merge" paths of multiple inheritance begun lower in the hierarchy. An obvious response is to simply remove all but the final occurrence of each duplicated concept. This turns the preceding list into:

buddy chihuahua small-thing dog pet animal living-thing thing

This list is called a linearization of the abstractions of the concept.

The algorithm for finding the value of an attribute a concept using a linearization is:

This algorithm works (with some caveats discussed later), but it has a very bad property: it has to create a list every time you search for an inherited attribute value. Getting values for attributes is probably the single most frequent activity that occurs in a frame system. We have to be more efficient here. Finding an attribute value for a concept has to be cheap.

Improving the algorithm

One solution is to create the linearizations for concepts when they are defined. This is a little tricky, because we have to handle concepts being defined and redefined in any order, but normally it's the way to go.

The algorithm works as follows:

Note that this assumes that the linearizations for the parents have already been calculated. This is true for all parents that have been defined explicitly. If we want to allow C to be defined with a parent p that has not yet been explicitly defined, then the linearization for p is simply the list of p, because p has no known parents.

The last step is critical for fixing anything changes that occur when concepts are redefined. This includes the case were we define a concept then later define one of its parents.

By calculating the linearizations in advance, the expensive steps of the algorithm are done once and for all, at definition time, before most retrieval occurs. Finding the value of an attribute is then just a simple, cheap list search.

We use this approach in the class frame system, using up some memory in order to get faster search times. The function all-absts-of returns the linearized abstractions of a concept.

A problem with the linearization algorithm

Appending all-absts-of and removing duplicates produces a list of concepts that does not violate the basic rules of inheritance. However, it can lead to surprising unintuitive results, as discovered and presented in "Proposal for a Monotonic Multiple Inheritance Linearization," by R. Ducournau, M. Habib, M. Huchard, and M.L. Mugnier, OOPSLA `94.

Consider their hierarchy (which is implemented in mop-examples.lisp):

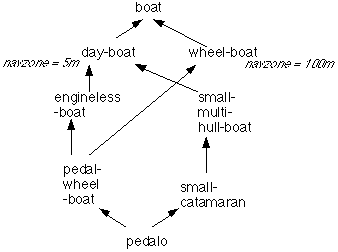
This is a hierarchy of various small boats, with one inheritable slot of interest, navzone, which says how far from harbor the boat can be taken.

Here's the surprising result. Using the "append and remove duplicates" algorithm,

It's not hard to see why this happens.

> (absts-of 'pedalo)
      (PEDAL-WHEEL-BOAT SMALL-CATAMARAN)

      > (all-absts-of 'pedal-wheel-boat)
      (PEDAL-WHEEL-BOAT ENGINELESS-BOAT DAY-BOAT WHEEL-BOAT BOAT THING)

      > (all-absts-of 'small-catamaran)
      (SMALL-CATAMARAN SMALL-MULTI-HULL-BOAT DAY-BOAT BOAT THING)

If we append those two abstraction lists, remove duplicates from left to right, and put PEDALO at the front, we get:

(PEDALO PEDAL-WHEEL-BOAT ENGINELESS-BOAT WHEEL-BOAT SMALL-CATAMARAN
      SMALL-MULTI-HULL-BOAT DAY-BOAT BOAT THING)

With this list, navzone 100m is the first value found.

Note that 100 is not wrong. In the chain of concepts between pedalo and wheel-boat, there is no value that overrides 100m. But it's clearly counterintuitive to have both parent concepts get one value and the child concept get another.

Clearly, we'd prefer an algorithm for linearizing that would lead to pedalo inheriting the same navzone as its parents. Ducournau et al. call an algorithm that tries to guarantee this property monotonic. The term "monotonic" is frequently used in artificial intelligence to refer to algorithms that have intuitive additive properties. This usage is inspired by the concept of "monotonically increasing functions" in mathematics.

A Monotonic Linearization Algorithm

Ducournau et al. had an alternative, somewhat complex, algorithm, that avoided this unintuitive behavior. In A Monotonic Superclass Linearization for Dylan," by Barrett, Cassels, Haahr, Moon, Playford, and Withington (OOPSLA '96, pp 69 - 82), an improved algorithm (called C3 for reasons not explained) was given. C3 has an additional advantage of paying attention to the order in which parents of a concept are listed. This is not as important for concept hierarchies as it is for programming, but since the C3 algorithm is also simple to describe, we'll use it here.

First, it helps to define a general list merging algorithm that merges zero or more lists LL into one list L using the following steps:

A concept linearization algorithm has to do two things:

A simple algorithm for linearizing the abstractions of concept c is to:

After merging, we add the original concept c to the front of the merged list and we're done.

An element x is "ready" if it only appears at the head of lists in LL, that is, it's not preceded by anything else in any list in LL.

For example, given the example pedalo hierarchy, this algorithm would initialize LL to

((pedal-wheel-boat engine-less day-boat wheel-boat boat)
      (small-catamaran small-multihull day-boat boat)
      )

The selection rule would first select pedal-wheel-boat and engine-less from the first list then, because day-boat isn't ready, it would select small-catamaran and small-multihull from the second list, and so on. The final linearization, with pedalo added to the front, would be:

(pedalo pedal-wheel-boat engine-less small-catamaran
         small-multihull day-boat wheel-boat boat)

You should verify this for yourself. The important thing to notice is that day-boat appears before wheel-boat in the final list, so therefore pedalo will inherit a navzone of 5m, just like its parents.

Another Linearization Problem

Barrett et al. however noticed that there are other hierarchies where this simple algorithm can still lead to unexpected results. In particular, consider the following hierarchy of graphical user interface objects:

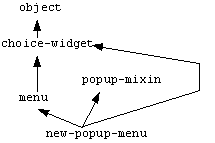
With this hierarchy, the simple algorithm would initialize LL to

((menu choice-widget object)
      (popup-mixin)
      (choice-widget object)
      )

The simple selection rule would generate the following list:

(menu choice-widget popup-mixin object)

Unfortunately, suppose the person defining new-popup-menu put popup-mixin before choice-widget in their definition of new-popup-menu in order to guarantee that properties of popup-mixin took precedence over properties of choice-widget. For them, the above linearization produces an unexpected result.

The C3 Linearization Algorithm

The C3 algorithm tries to fix this problem by making one change to the simple algorithm. C3 initializes LL to:

Thus, for new-popup-menu, LL would be initialized to

((menu popup-mixin choice-widget)
      (menu choice-widget object)
      (popup-mixin)
      (choice-widget object)
      )

Now the simple selection rule will select popup-mixin before choice-widget, as expected by the definer of new-popup-menu.

A Problem (?) with the C3 Algorithm

The simple algorithm produces an unexpected result for new-popup-menu if you don't realize that choice-widget is a parent of menu. As a rule, our programmers and knowledge engineers shouldn't have to know how a concept hierarchy is organized internally in order to add new concepts at the bottom, especially since those internal relationships may change over time. This is one of the arguments for the C3 modification to the simple algorithm.

Unfortunately, the C3 modification, at least as described in Barrett et al., can also produce unexpected results. Consider this hierarchy, where the definer wanted to make sure choice-widget properties took precedence:

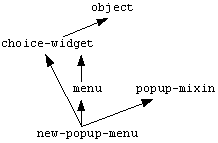
The C3 algorithm would initialize LL to

((choice-widget menu popup-mixin)
      (choice-widget object)
      (menu choice-widget object)
      (popup-mixin)
      )

Now the simple selection rule will be unable to select anything, because neither choice-widget, menu, nor popup-mixin is "ready." The C3 algorithm thinks the hierarchy has some cycles in it, but it doesn't. It's the order of parents that's a problem. You can't make choice-widget override menu because menu is more specific than choice-widget. On the other hand, choice-widget properties can take precedence over popup-mixin.

There's no way to give the definer exactly what they want. One compromise is to check to see if the list of parents has a class before a subclass. If so, ignore that class when doing the cycle check and picking the next item. In the above case, we'd pick menu, even though it's behind choice-widget because it's only behind in the parent list. menu is not a superclass of choice-widget. We'd update LL to 

((choice-widget popup-mixin)
      (choice-widget object)
      (choice-widget object)
      (popup-mixin)
      )

so choice-widget would be picked next, over popup-mixin, as the definer intended.